O Problema dos Três Corpos: Uma Dança Gravitacional Complexa

Muita gente deve ter ficado curiosa ao assistir à série “O problema dos 3 corpos” da Netflix e de ve ter ficado intrigada sobre o problema real que dá nome à serie (e à série de livros) que é de origem astronômica. Fato é que o universo é repleto de fenômenos fascinantes e desafiadores, e um dos mais intrigantes, sem dúvida, é o Problema dos Três Corpos.

O problema: Imagine três corpos celestes, como planetas ou estrelas, orbitando uns aos outros sob a influência de suas próprias forças gravitacionais. O movimento desses corpos é regido pelas leis da física, especialmente pela Lei da Gravitação Universal de Newton. No entanto, mesmo com essas leis bem estabelecidas, o Problema dos Três Corpos desafia nossa capacidade de prever com precisão o comportamento dos componentes do sistema.

O problema dos 3 corpos foi originalmente proposto por Isaac Newton em 1687. Ele foi capaz de encontrar soluções analíticas para o caso especial de três corpos que estão em uma configuração triangular. No entanto, o problema geral de três corpos não foi resolvido analiticamente até o século 20.

Vamos considerar um exemplo simplificado do Problema dos Três Corpos, onde temos três corpos de massa igual, denominados A, B e C, que interagem entre si apenas pela força gravitacional.

As equações diferenciais que descrevem o movimento de cada corpo podem ser expressas usando as Leis de Newton da Gravitação Universal:

Para o corpo A:

Onde:

• é a constante gravitacional,
• e são as massas dos corpos B e C, respectivamente,
• , e são as coordenadas cartesianas dos corpos A, B e C, respectivamente, e
• e são as distâncias entre os corpos A e B, e A e C, respectivamente.

As equações para os corpos B e C são análogas.

Para resolver numericamente essas equações e prever o movimento dos corpos ao longo do tempo, podemos usar métodos como o método de Euler ou o método de Runge-Kutta.

No entanto, devido à natureza não linear do problema e à sensibilidade às condições iniciais, a previsão a longo prazo do movimento dos corpos pode se tornar imprecisa, especialmente para sistemas complexos ou instáveis. Portanto, simulações computacionais detalhadas são frequentemente necessárias para entender o comportamento dos sistemas de três corpos.

Uma das principais razões para a dificuldade do problema é sua grandiosa complexidade matemática. As equações que descrevem o movimento dos corpos são altamente não lineares e não têm solução analítica para o caso geral (n-corpos). Isso significa que não há uma fórmula matemática simples que possa prever o movimento dos corpos ao longo do tempo. Em vez disso, os cientistas precisam recorrer a métodos numéricos e simulações por computador para estudar o problema.

Além da complexidade matemática, o Problema dos Três Corpos exibe comportamento caótico e é altamente sensível às condições iniciais. Isso significa que pequenas variações nas posições ou velocidades iniciais dos corpos podem levar a resultados significativamente diferentes ao longo do tempo. Essa sensibilidade dificulta ainda mais a previsão precisa do movimento dos corpos.

Embora o Problema dos Três Corpos seja desafiador, ele tem amplas aplicações em diversas áreas da ciência, incluindo astronomia, física e engenharia espacial. O estudo desse problema nos ajuda a entender melhor o comportamento dos sistemas gravitacionais complexos no universo e pode fornecer insights importantes para o desenvolvimento de futuras missões espaciais.

O Problema dos Três Corpos continua sendo um dos desafios mais intrigantes e complexos da física. Apesar de sua dificuldade, os cientistas continuam a explorar e estudar esse problema, utilizando métodos avançados de computação e simulação para desvendar os segredos da dança gravitacional dos corpos celestes no universo.

Em uma simulação, em python disponível no Github (em 2D) podemos ver o seguinte gráfico do movimento dos 3 corpos:

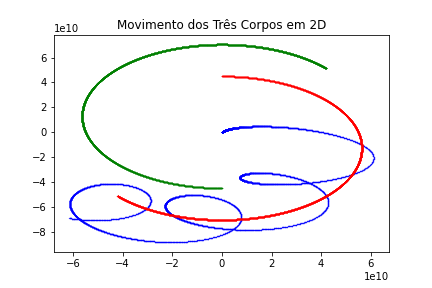
O que confirma o movimento caótico dos corpos a partir das condições iniciais.

SOBRE A SÉRIE: A série da Netflix é uma adpatação do romance homônimo de Liu Cixin, que ganhou o Prêmio Hugo de Melhor Romance em 2015. O livro conta a história de uma astrofísica chinesa que se envolve em uma investigação secreta relacionada ao problema dos 3 corpos e à possível invasão da Terra por uma civilização alienígena. Na minha opinião, vale a audiência de quem, como eu, curte ficção científica.

Tratando “warning: ignoring return value of ‘scanf’” no compilador gcc do Replit.com (e no Unix-like)

Boa parte das pessoas que começaram a aprender a programar seja em cursos online, presenciais, faculdades e escolas de programação já se deparou com o Replit.com.

O Replit.com é uma plataforma de criação de software que oferece um IDE (Ambiente de Desenvolvimento Integrado), recursos de inteligência artificial e a capacidade de implantar projetos diretamente do navegador. No Replit, você pode gerar, editar e explicar código, colaborar em tempo real e implantar seus projetos diretamente do navegador. É uma ferramenta útil para programadores e educadores, pois permite programar em várias linguagens de programação, como Java, Python, C, C++, entre outras, e é acessível em qualquer dispositivo sem a necessidade de configuração (e o melhor você pode PUBLICAR seu projeto de software – qualquer um!). Eu uso bastante em sala de aula (seja para C, Java, Python ou desenvolvimento Web).

Quem já usou o Replit.com para programar em C (ou aprender a programar ou testar códigos na linguagem C) eventualmente já se deparou com o erro:

warning: ignoring return value of ‘scanf’ declared with attribute ‘warn_unused_result’ [-Wunused-result]

Este erro (na verdade, uma warning) ocorre pela definição de scanf do compilador usar o atributo específico do GCC (warn_unused_result). De algum modo os desenvolvedores da biblioteca C decidiram que o valor de retorno de scanf não deve ser ignorado na maioria dos casos, então eles deram a ele um atributo informando ao compilador para dar um aviso quando você não o usa.

O problema é que na imensa maioria dos casos você não vai lidar (diretamente) com o valor de retorno de scanf. De modo que este é um aviso que você poderá ignorar quase sempre.

Para desativar a warning você pode compilar usando a opção -Wno-unused-result, assim:

gcc nome_do_arquivo.c -o nome_do_arquivo.out -Wno-unused-result

Infelizmente este método te obrigará a setar a flag SEMPRE que for compilar cada arquivo individualmente. Para que você não precise inserir a flag na compilação (e se usa o maravilhoso Make para isso) você pode editar o seu Makefile e inserir essa opção nas flags da compilação, por exemplo, da seguinte forma:

override CFLAGS += -g -Wno-everything -pthread -lm -Wno-unused-result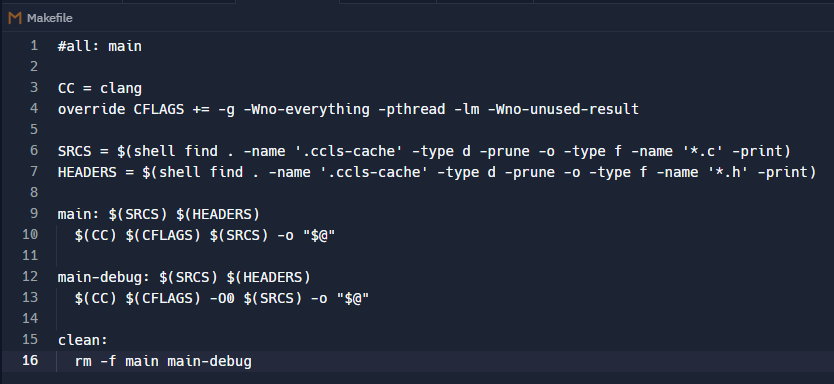

Deste modo sempre que usar o make nomedoarquivo para compilar o arquivo (ou projeto) o compilador ignorará a warning e você não precisará, digamos, lidar com o valor de retorno de scanf.

7 sites para download de Música de Videogames de graça (free video game music)

A música de videogame é incrivelmente icônica. Para os jogos mais antigos, evoca nostalgia da infância e de uma época mais simples. Jogos mais recentes muitas vezes contam com músicos mundialmente famosos colaborando nas trilhas sonoras. E há uma grande quantidade de conteúdo entre eles que atrai tanto fãs casuais quanto jogadores hardcore.

Mas onde você pode encontrar músicas de videogame? Se você quer reviver trilhas sonoras de jogos sem o estresse de jogar o jogo em si, confira esses principais sites.

Pseudocódigo. Outra forma de representar algoritmos

Nós já vimos duas das principais formas de representar algoritmos, a descrição narrativa e os fluxogramas. Hoje vamos ver a terceira.

A representação e descrição de algoritmos é uma parte fundamental da programação. Ela permite que os desenvolvedores comuniquem de forma clara e concisa a lógica e os passos necessários para resolver um problema ou realizar uma tarefa. O pseudocódigo é uma forma de representação de algoritmos que combina elementos de linguagem de programação com linguagem natural, tornando-o mais compreensível para humanos, independentemente da linguagem de programação específica.

O pseudocódigo não é uma linguagem de programação real, mas sim uma maneira de descrever a sequência de passos lógicos de um algoritmo. Ele utiliza convenções e estruturas de controle semelhantes às linguagens de programação, como declarações condicionais, loops e instruções de atribuição, permitindo que o desenvolvedor descreva a lógica de um algoritmo de maneira clara e estruturada.

Vamos considerar um exemplo simples para ilustrar o uso do pseudocódigo. Suponha que queremos escrever um algoritmo para calcular a média aritmética de três números. Utilizando pseudocódigo, poderíamos representar o algoritmo da seguinte forma:

1. Ler três números (num1, num2, num3)
2. Calcular a soma dos três números (soma = num1 + num2 + num3)
3. Calcular a média (media = soma / 3)
4. Exibir a média

Nesse exemplo, cada linha descreve uma etapa do algoritmo. Na linha 1, estamos lendo os três números, e na linha 2, calculamos a soma dos três números. Em seguida, na linha 3, calculamos a média dividindo a soma pelo número de elementos (3). Por fim, na linha 4, exibimos o resultado da média.

O pseudocódigo permite que o desenvolvedor se concentre na lógica do algoritmo, independentemente da sintaxe de uma linguagem de programação específica. Isso facilita a compreensão e a comunicação do algoritmo entre os membros da equipe de desenvolvimento.

Além disso, o pseudocódigo é altamente flexível e pode ser adaptado de acordo com as necessidades do projeto. Por exemplo, se desejarmos adicionar uma verificação de erro para garantir que os números inseridos sejam válidos, poderíamos modificar o pseudocódigo da seguinte maneira:

1. Ler três números (num1, num2, num3)
2. Verificar se os números são válidos
   2.1. Se algum número for inválido, exibir uma mensagem de erro e encerrar o programa
3. Calcular a soma dos três números (soma = num1 + num2 + num3)
4. Calcular a média (media = soma / 3)
5. Exibir a média

Nesse caso, adicionamos uma etapa extra (2) para verificar se os números são válidos. Se algum número for inválido, exibimos uma mensagem de erro e encerramos o programa. Essa modificação pode ser facilmente realizada no pseudocódigo, sem se preocupar com a sintaxe de uma linguagem de programação específica.

O uso de pseudocódigo também é comum em documentação técnica e algoritmos complexos, onde a compreensão do fluxo lógico é essencial. Ele pode ser facilmente convertido em código real em uma linguagem de programação específica, pois o pseudocódigo é projetado para ser independente de uma linguagem em particular.

Basicamente, o pseudocódigo é uma forma eficaz de representar e descrever algoritmos. Ele combina elementos de linguagem de programação com linguagem natural, permitindo que os desenvolvedores expressem a lógica do algoritmo de forma clara e estruturada. O pseudocódigo facilita a comunicação, a compreensão e a implementação dos algoritmos, independentemente da linguagem de programação utilizada.

Portugol

A representação e descrição de algoritmos utilizando o pseudocódigo conhecido como Portugol é uma prática amplamente utilizada no ensino e aprendizado de programação. O Portugol é uma linguagem de programação simplificada que permite aos iniciantes compreenderem a lógica e a estrutura dos algoritmos de forma mais clara e intuitiva, sem se preocuparem com a sintaxe complexa de linguagens de programação reais.

Ao utilizar o Portugol para representar algoritmos, é possível descrever passos sequenciais, estruturas condicionais e repetições de forma fácil e compreensível. Vamos considerar um exemplo simples de cálculo de média aritmética utilizando o Portugol:

Algoritmo "CalculaMedia"
   Var
      num1, num2, num3, soma, media: Real

   Início
      Escreva("Digite o primeiro número: ")
      Leia(num1)

      Escreva("Digite o segundo número: ")
      Leia(num2)

      Escreva("Digite o terceiro número: ")
      Leia(num3)

      soma <- num1 + num2 + num3
      media <- soma / 3

      Escreva("A média é: ", media)
   Fim

Neste exemplo, utilizamos o pseudocódigo Portugol para representar um algoritmo que lê três números, calcula a soma e a média aritmética dos mesmos, e exibe o resultado. As palavras-chave “Algoritmo”, “Var”, “Início” e “Fim” são utilizadas para definir a estrutura básica do algoritmo em Portugol.

Dentro da estrutura do algoritmo, utilizamos comandos como “Escreva” para exibir mensagens na tela, “Leia” para receber valores digitados pelo usuário, e os operadores matemáticos para realizar os cálculos necessários.

O uso do pseudocódigo Portugol é especialmente útil para iniciantes na programação, pois permite que eles se concentrem na lógica e na sequência de passos necessários para resolver um problema, sem se preocuparem com os detalhes específicos de uma linguagem de programação real. Dessa forma, os iniciantes podem aprender a estrutura básica dos algoritmos e ganhar confiança antes de se aventurarem em linguagens de programação mais complexas.

É importante ressaltar que o Portugol é apenas uma representação simplificada e não é executável diretamente. Ele serve como um meio de compreensão e aprendizado dos conceitos fundamentais da programação. Uma vez que o algoritmo tenha sido representado em Portugol, é possível traduzi-lo para uma linguagem de programação real, como Java, Python ou C, para que possa ser compilado e executado.

Como exemplo de pseudocódigos (em formas de programas) temos o Visualg (que usa uma versão do Portugol mais parecida com a usada no texto) e o Portugol Studio.

Até a próxima.

Recursividade: a multiplicação recursiva, as definições matemáticas por indução/recursão e os axiomas de Peano

A recursividade, como já vimos anteriormente deve primeiro sempre ser pensada nos casos mais simples (os casos bases ou casos básicos). Vamos ver um exemplo para nos ajudar.

É possível, por exemplo, definir a multiplicação de dois números inteiros m e n, sendo n > 0, em termos da operação de adição. O caso mais simples dessa operação é aquele no qual n = 0. Nesse caso, o resultado da operação é igual a 0, independentemente do valor de m. De acordo com a idéia exposta acima, precisamos agora pensar em como podemos expressar a solução desse problema no caso em que n > 0, supondo que sabemos determinar sua solução para casos mais simples, que se aproximam do caso básico. Neste caso, podemos expressar o resultado de m × n em termos do resultado da operação, mais simples m × (n − 1); ou seja, podemos definir m × n como sendo igual a m + (m × (n − 1)),
para n > 0. Ou seja, a operação de multiplicação pode então ser definida indutivamente pelas seguintes equações:

• ,

• 

Uma maneira alternativa de pensar na solução desse problema seria pensar na operação de multiplicação m * n como a repetição, n vezes, da operação de adicionar m, isto é:

• 

Raciocínio análogo pode ser usado para expressar a operação de exponenciação, com expoente inteiro não-negativo, em termos da operação de multiplicação (que será visto em outro post).

“Para entender a recursão, a pessoa deve primeiro entender a recursão.”

O programa a seguir apresenta, na linguagem C, uma forma computar o resultado da multiplicação de dois números, dados como argumentos dessas operações de forma recursiva. As função multiplica é definida usando-se chamadas à própria função, razão pela qual ela é chamada de recursiva.

int multiplica(int num1, int num2){
    //multiplicação por zero
    if (num1 == 0 || num2 == 0) {       
        return 0;
    }
    //caso base, onde a recursão para:
    else if (num2 == 1) {        
        return num1;
    }
    //multiplicando através da soma com recursividade:
    else {        
        return (num1 + multiplica(num1,num2 - 1));        
    }
}

Considere a função multiplica definida acima. A sua definição espelha diretamente a definição recursiva da operação de multiplicação, em termos da adição, apresentada anteriormente. Ou seja, multiplicar m por n  (onde n é um inteiro não-negativo) fornece:

• 0, no caso base (isto é, se n==0);
• m + multiplica(m, n-1), no caso indutivo/recursivo (isto é, se n!=0).

Vejamos agora, mais detalhadamente, a execução de uma chamada multiplica(3,2). Cada chamada da função multiplica cria novas variáveis, de nome m e n. Existem, portanto, várias variáveis com nomes (m e n), devido às chamadas recursivas. Nesse caso, o uso do nome refere-se à variável local ao corpo da função que está sendo executado. As execuções das chamadas de funções são feitas, dessa forma, em uma estrutura de pilha. Chamamos, genericamente, de estrutura de pilha uma estrutura na qual a inserção (ou alocação) e a retirada (ou liberação) de elementos é feita de maneira que o último elemento inserido é o primeiro a ser retirado.

Em resumo, na tabela abaixo, representamos a estrutura de pilha criada pelas chamadas à função multiplica. Os nomes m e n referem-se, durante a execução, às variáveis mais ao topo dessa estrutura. Uma chamada recursiva que vai começar a ser executada está indicada por um negrito. Nesse caso, o resultado da expressão, ainda não conhecido, é indicado por “…”.

---

Tabela 4.2: Passos na execução de multiplica(3,2)

Comando/Expressão	Resultado (expressão)	Estado (após execução/avaliação)
multiplica(3,2) …		m↦ 3 n↦ 2
n == 0	falso	m↦ 3 n↦ 2
return m + multiplica(m,n-1)	…	m↦ 3   m↦ 3 n↦ 2   n↦ 1
n == 0	falso	m↦ 3   m↦ 3 n↦ 2   n↦ 1
return m + multiplica(m,n-1)	…	m↦ 3   m↦ 3   m↦ 3 n↦ 2   n↦ 1   n↦ 0
n == 0	verdadeiro	m↦ 3   m↦ 3   m↦ 3 n↦ 2   n↦ 1   n↦ 0
return 0		m↦ 3   m↦ 3 n↦ 2   n↦ 1
return m + 0		m↦ 3 n↦ 2
return m + 3
multiplica(3,2)	6

E assim vemos como o procedimento recursivo para multiplicar dois números funciona com um exemplo em linguagem C, facilmente portável para outra linguagem.

Agora, para uma visão matematicamente mais precisa, continue lendo…

---

Definições por indução

As definições por indução (usando o princípio da indução dos axiomas de Peano) se baseiam na possibilidade de se iterar uma função um número arbitrário , n, de vezes.

Mais precisamente, seja uma função cujo domínio e contradomínio são o mesmo conjunto . A cada podemos, de modo único, associar uma função de tal maneira que . Em particular, se chamarmos , teremos . (lembrando que s(n) é o sucessor de um número natural n, conforme descrito nos axiomas de Peano).

Numa exposição mais, digamos, sistemática da teoria dos números naturais, a existência da n-ésima iterada de uma função é um teorema, chamado (lindamente) de “Teorema da Definição por Indução”.

É importante ressaltar que não é possível, nesta altura, definir simplesmente como pois “n vezes” é uma expressão sem sentido no contexto dos Axiomas de Peano, já que um número natural n é, por enquanto, apenas um elemento do conjunto (um número ordinal), sem condições de servir de resposta à pergunta “quantas vezes”?, até que lhe seja dada a condição de número cardinal.

Admitamos assim que, dada uma função , sabemos associar, de modo único, a cada número natural , uma função , chamada a n-ésima iterada de f, de tal modo que .

Agora, podemos ver um exemplo de definição por indução (recursão) usando o que acabamos de ver, as iteradas da função . Vamos ver o produto de números naturais (semelhantemente a soma e a exponenciação podem ser definidas da mesma forma). Sigamos com a multiplicação… (que vimos acima de forma menos formal e mais voltada para a lógica da programação)… Vejamos.

O produto, a multiplicação, de dois números naturais é definido da seguinte forma:

e

Em outras palavras: multiplicar um número por não o altera. Multiplicar por um número maior do que , ou seja, por um número da forma , é iterar a operação de somar , começando com .

Assim, por exemplo, ; e

.

Lembrando a definição de , vemos que o produto está definido indutivamente (ou recursivamente) pelas propriedades abaixo:

,

.

Que é exatamente a mesma definição recursiva que vimos acima!

Fermat, o cálculo integral, quadraturas de curvas e comunicação acadêmica

É lugar-comum que o Cálculo Diferencial e Integral foi “descoberto” simultânea e independentemente por Isaac Newton (1643-1727) e Leibniz (1646-1716), individualmente, cada um a seu modo, diante de problemas semelhantes, mas com interpretações, definições e nomenclaturas totalmente diferentes. Newton, como físico, estava preocupado inicialmente com os problemas de taxas de variação do movimento e Leibiniz buscava algo mais, digamos, “abstrato” e puramente matemático (baseado no problema da tangente em pontos de curvas, ao fim e ao cabo o mesmo problema da taxa de variação). Newton chamava a variação (ou, modernamente, a derivada) de “fluxões” e sua nomenclatura não sobreviveu (a de Leibniz era muito mais robusta).

Poucos sabem, inclusive, que as primeiras edições do “Método das Fluxões” de Newton citava Leibniz e seu método. Após a controvérsia do cálculo, obviamente nas edições posteriores isso foi retirado. O fato é que, por conta da falta de comunicação acadêmica na época (méados do século XVII), muitos cientistas e matemáticos estiveram bem próximos de ter o “insight” do Cálculo diferencial e integral, ou seja, juntar todos os pontos e apresentar algo geral que funcionasse para outros problemas de variação e áreas (que foi o que Newton e Leibiniz fizeram, apresentaram métodos para o problema das taxas de variação (tangentes) e de áreas sob curvas que poderiam ser generalizados para outros problemas semelhantes).

Pierre de Fermat (1607-1665)

Pierre de Fermat (1601-1665) foi um deles. Este post mostra o quão perto ele estava de apresentar uma gênese do cálculo integral. Precisamos, claro, de contexto. Se você não quer saber do contexto histórico pode pular a parte do contexto.

---

Vamos lá… O problema de encontrar a área de uma forma plana fechada é conhecido por quadratura. A palavra refere-se à própria natureza da problema: expressar a área em termos de unidades de área, que são quadrados. É um problema que remonta aos gregos antigos e diversos nomes são famosos pelas soluções aproximadas do problema, como Arquimedes (e seu método da exaustão). Mas os gregos não consideravam o infinito como o consideramos hoje (e os paradoxos de Zenão são uma prova disto).

Por volta de 1600, processos infinitos foram introduzidos na matemática e, então, o problema da quadratura tornou-se meramente computacional. O próprio círculo, por esta época, já estava bem definido em relação à sua quadratura (ou área que envolvia a constante irracional ), mas a hipérbole era uma das curvas que resistia a todas as tentativas de quadratura.

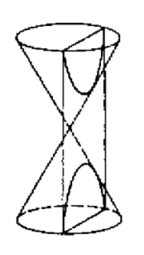
A hipérbole é a curva obtida quando um cone é cortado por um plano num ângulo maior do que o ângulo existente entre a base do cone e o seu lado (daí o prefixo “hiper” significando “em excesso de”). O cone (e o corte) sendo algo como a figura abaixo:

cônica gerando a hipérbole

Como resultado deste corte, a hipérbole fica com dois “ramos” separados e simétricos. O resultado é a imagem abaixo:

A hiperbole retangular

Percebe-se, pela imagem acima que a hipérbole tem um par de linhas retas associadas a ela, suas duas linhas tangentes no infinito. Quando se move ao longo de cada “ramo”, afastando-se do centro, nos aproximamos cada vez mais destas linhas, mas nunca a alcançamos. Essas linhas são as assíntotas da hipérbole. São, grosso modo, a manifestação geométrica do conceito de limite, base do cálculo diferencial e integral.

Os gregos trabalhavam com as curvas de um ponto de vista puramente geométrico, mas a invenção da geometria analítica por Descartes (1596-1650) fez com que o estudo dessas curvas se tornassem cada vez mais parte da álgebra. No lugar da curva em si, considera-se, então, a equação que relaciona as coordenadas x e y de um ponto da curva.

Descartes (1596-1650)

Cada uma das seções cônicas é um caso especial de uma equação quadrática (de segundo grau), cuja forma geral é: .

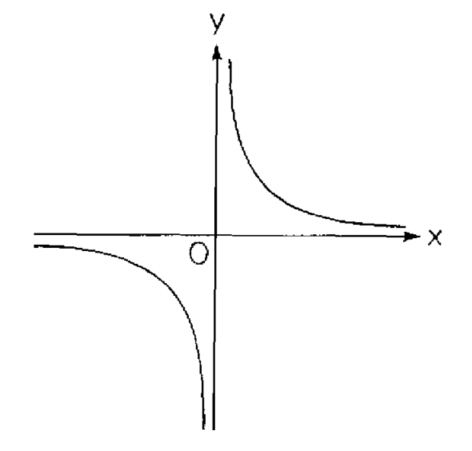
Para o círculo, por exemplo, temos que e , assim chegamos, então, à equação cujo gráfico é um círculo com centro na origem e raio 1 (o círculo unitário). A hipérbole mostrada na figura acima corresponde ao caso e ; e sua equação é , ou o equivalente . Suas assíntotas são, portanto, os eixos x e y. Esse tipo de hiperbole é conhecida como hipérbole regular.

Finalizando o contexto, sabe-se que Arquimedes não conseguiu encontrar a quadratura da hipérbole pelo método da exaustão. Também o métodos dos indivisíveis não alcançou este objetivo, principalmente porque a hipérbole, ao contrário do círculo e da elipse, é uma curva que vai ao infinito, assim é preciso esclarecer o que queremos dizer por quadratura neste caso.

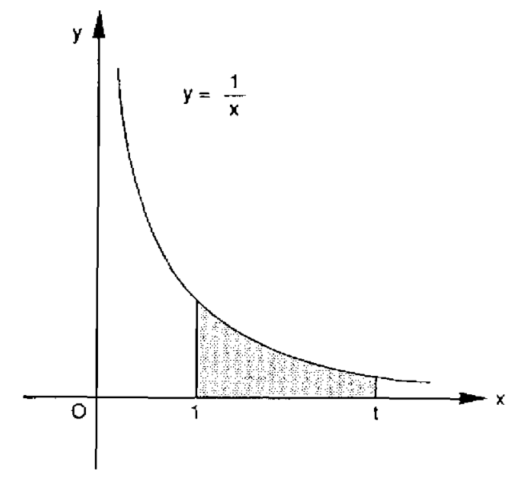
A figura abaixo mostra um ramo da hipérbole . No eixo dos x nós marcamos o ponto fixo e o ponto arbitrário . Por área sob a hipérbole queremos nos referir à área entre o gráfico de , o eixo dos x e as linhas verticais (ordenadas) e . É claro que o valor numérico desta área ainda vai depender de nossa escolha de t, sendo, portanto, uma função de t. Vamos chamar essa função de . O problema da quadratura da hipérbole resume-se a encontrar esta função, isto é, exprimir a área como uma fórmula envolvendo a variável t.

A área sob a hipérbole retangular de a

Vários matemáticos tentaram resolver este problema de forma independente (mais uma vez a falta de clareza na “comunicação acadêmica” – que sequer existia, atrapalhava a matemática e a ciência). Os mais destacados foram os já citados, Descartes e Fermat, além de Pascal (1623-1662). Os 3 são o grande triunvirato francês nos anos que antecederam a invenção do Cálculo infinitesimal (outro nome para o cálculo diferencial e integral). Fim do Contexto.

---

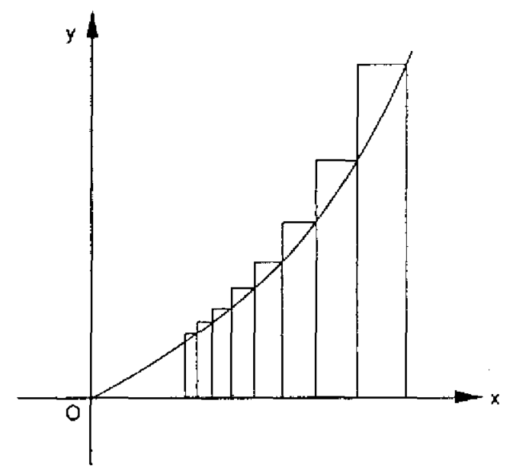
Fermat estava interessado na quadratura de curvas cuja equação geral é , onde n é um inteiro positivo. Essas curvas são às vezes chamadas de parábolas generalizadas (a própria parábola é o caso ). Ele fez a aproximação da área sob cada curva através de uma série de retângulos cujas bases formam uma progressão geométrica decrescente. Isto é muito semelhante ao método da exaustão de Arquimedes, mas ao contrário de seu predecessor, Fermat não evitou recorrer a uma série infinita. A figura abaixo mostra uma porção da curva entre os pontos e no eixo dos x.

O método de Fermat de aproximação da área sob o gráfico de através de uma série de retãngulos, cujas bases formam uma progressão geométrica

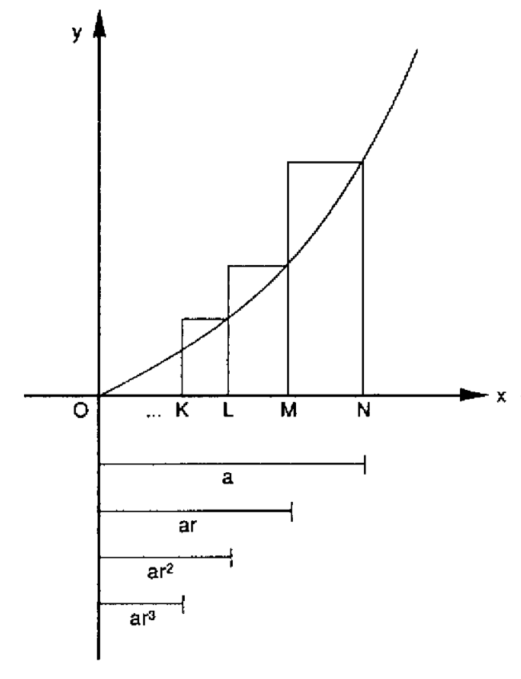
Fermat, então, imaginou o intervalo entre e como sendo dividido em um número infinito de subintervalos pelos pontos … , onde . Então, começando em N e trabalhando no sentido inverso, para que esses intervalos formem uma P.G. decrescente, se tem , , , e assim por diante, onde r é menor do que 1. Assim, as alturas (eixo das ordenadas y) da curva nesses pontos são , , , etc. A partir daí é fácil encontrar a área de cada retângulo e então somar as áreas, usando a fórmula do somatório para uma série geométrica infinita. A fórmula resultante é:

(1) ,

onde o r subscrito em A indica que a área ainda depende de nossa escolha de . Fermat então raciocinou que, de modo a melhorar o encaixe entre os retângulos e a curva verdadeira, a largura de cada retângulo devia se tornar bem pequena como na figura abaixo:

Uma aproximação melhor pode ser obtida fazendo os retângulos menores enquanto se aumenta o número

Para conseguir isso, a proporção comum r deve se aproximar de 1, e quanto mais próxima, melhor o “encaixe” (e mais fácil a soma). Aliás, quando r → 1 (r tende ao valor 1), a equação 1 torna-se a expressão indeterminada 0/0. Fermat foi capaz de contornar essa dificuldade notando que o denominador da equação 1 acima, , pode ser escrito na forma fatorada, como .

Quando o fator no numerador e no denominador é cancelado, a equação 1 torna-se:

Quando deixamos r → 1, cada parcela no denominador tende a 1, o que resulta na fórmula

(2)
Todo estudante de cálculo vai reconhecer a equação 2 como a integral . A famosa integral do monômio.

Fermat trabalhou nessa ideia em torno de 1640, cerca de 30 anos antes de Newton e Leibniz estabelecessem esta mesma fórmula como parte de seus respectivos cálculo diferencial e integral. Este trabalho representou MUITO porque conseguia a quadratura não apenas de uma curva, mas de toda uma família de curvas, aquelas fornecidas pela equação para valores inteiros, positivos de n.

Interessante notar que quando , a fórmula dá o que é exatamente o resultado obtido por Arquimedes pelo método da exaustão para a a párabola.

O mais incrível de tudo é que, ao modificar ligeiramente seu procedimento, Fermat mostrou que a equação 2 permanece válida mesmo quando n é um inteiro negativo , desde que agora calculemos a área de x = a (onde a > 0) até o infinito. Quando n é um inteiro negativo, digamos (onde m é positivo), obtemos a família de curvas , chamadas de hipérboles generalizadas. Que a fórmula de Fermat funcione mesmo nesse caso é notável, já que as equações e , apesar de sua aparente semelhança, representam tipos bem diferentes de curvas: as primeiras são contínuas em toda a parte, enquanto as últimas se tornam infinitas em e em, portanto, possuem uma “quebra” (uma assíntota vertical) neste ponto.

Fermat ficou muito contente com sua descoberta porque ela permanecia válida mesmo quando a restrição de n ser positivo era removida. Mas, havia um problema. problema. A fórmula de Fermat falhava para uma curva da qual toda a família deriva o seu nome: a hipérbole . Isso ocorre porque para , o denominador na equação 2 se torna 0. A frustração de Fermat por não ser capaz de cobrir este caso tão importante deve ter sido grande, mas ele a escondeu atrás de palavras simples. “Eu digo que todas essas hipérboles infinitas, exceto a de Apolônio (a hipérbole ), ou a primeira, podem ser quadradas pelo método da progressão geométrica, de acordo com um procedimento geral e uniforme”.

Quem resolveu este problema foi um dos contemporâneos de Fermat, embora pouco conhecido. Grégoire de Saint-Vicent (1584-1667), um jesuíta belga que trabalhou a maior parte da vida trabalhando em problemas de quadratura.

Seu principal trabalho, Opus geometricum quadraturae circuli et sectionum coni (1647), foi compilado a partir de milhares de textos científicos que Saint-Vincent deixou para trás quando fugiu de Praga ante o avanço dos suecos em 1631. Eles foram resgatados por um colega e devolvidos ao autor dez anos depois. O atraso na publicação torna difícil estabelecer a primazia de Saint-Vincent com certeza absoluta, mas parece que ele foi o primeiro a notar que, quando , os retângulos usados na aproximação da área sob a hipérbole possuem, todos, áreas iguais.

A imagem abaixo mostra que que, conforme a distância de 0 cresce geometricamente, as áreas correspondentes crescem em incrementos iguais — ou seja, aritmeticamente — e isso continua sendo verdade mesmo ao passarmos ao limite quando r → 1 (ou seja, quando fazemos a transição dos retângulos discretos para a hipérbole contínua). Mas isso, por sua vez, implica que a relação entre a área e a distância é logarítmica. Mais precisamente, se denotarmos por A(t) a área sob a hipérbole, a partir de um ponto de referência fixo x > 0 (por conveniência geralmente escolhemos x = 1) até um ponto variável x = t, teremos A(t) = log t. Um dos alunos de Saint-Vincent, Alfonso Anton de Sarasa (1618-1667), escreveu essa relação explicitamente registrando uma das primeiras ocasiões em que se fez o uso de uma função logarítmica (que eram, prioritariamente, uma ferramenta usada para cálculos complexos).

Quando as bases formam uma PG, os retângulos possuem áreas iguais. A área é proporcional ao logaritmo da distância horizontal

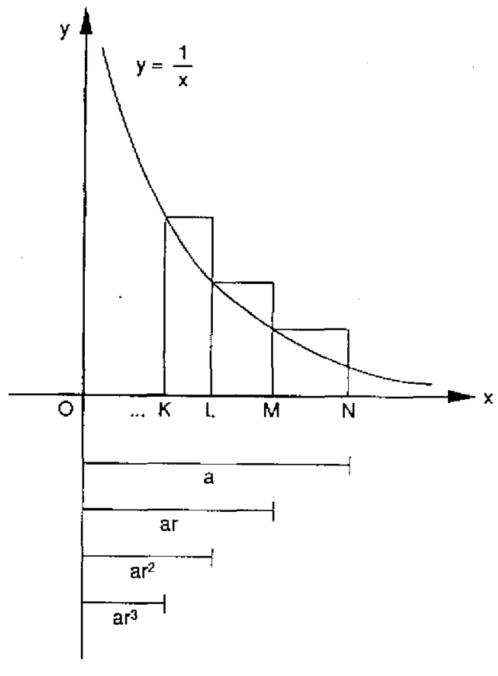
Assim, a quadratura da hipérbole foi finalmente conseguida cerca de dois mil anos depois dos gregos, que primeiro enfrentaram o problema.

Portanto, quando Newton e Leibniz se debruçaram sobre os problemas que os levariam independepentemente à invenção da mais incrível e impressionante ferramenta científica de todos os tempos (o Cálculo diferencial e integral), as princiais ideias por trás do Cálculo já eram razoavelmente bem conhecidas pela comunidade matemática. O método dos indivisíveis, embora repousando em uma base incerta, tinha sido aplicado com sucesso a um conjunto de curvas e sólidos; e o método da exaustão de Arquimedes, em sua forma moderna, revisada, resolvera a quadratura da família de curvas . Embora esses métodos fossem bem-sucedidos, eles ainda não estavam reunidos em um sistema único; cada problema exigia uma abordagem diferente e o sucesso dependia da engenhosidade geométrica, habilidades com a álgebra e uma boa dose de sorte. O que se precisava era de um procedimento geral e sistemático — um conjunto de algoritmos — que permitiriam resolver esses problemas com facilidade e eficiência. Este procedimento foi fornecido por Newton e Leibniz.

O ponto é que estas ferramentas teriam sido desenvolvidas, provavelmente, muito antecipadamente se existisse, à época, como hoje, uma comunidade científica vibrante e atuante, com publicações compartilhadas e o conhecimento sendo construído sobre as bases do que se fez anteriormente.

Problemas de comunicação e, principalmente, locomoção e transporte, claro, afetavam isso, mas a postura de cientistas, como Newton que guardavam para si seus trabalhos (ele só publicou o seu cálculo quando viu que o que Leibniz havia publicado era, ao fim e ao cabo, o mesmo que ele tinha conseguido), atrapalhavam bastante o avanço das contribuições.

O que teria acontecido (sabe-se que a revolução científica, de fato, começou com a invenção do cálculo e a normatização do método científico) se a comunicação acadêmica tivesse levado à invenção do cálculo alguns anos, décadas ou séculos antes do que o que realmente o foi?

…

Nunca saberemos. Mas, gosto de pensar que os avanços científicos teriam sido acelerados enormemente…

Guia de configuração do ambiente de desenvolvimento nativo do Windows para usuários do Linux

Encontrei um repositório excelente com um Guia de configuração do ambiente de desenvolvimento nativo do Windows para usuários do Linux. As dicas são muito interessantes e valem para todos os developers.

Segue o link: https://github.com/rkitover/windows-dev-guide

Enjoy!

Renomeando diversos arquivos retirando partes deles no Mac (ou Linux)

Enfrentei um problema ao me deparar com uma cópia de múltiplos (centenas) de arquivos realizada de um hd externo com conteúdo em NTFS para outro em FAT32 que estava em um Mac. Usei um utilitário chamado WinSCP (copiava através de uma máquina com um Windows 10 via SSH).

Os arquivos foram corretamente copiados, mas, ao final, centenas deles (por não terem sido possível de serem renomeados pelo WinSCP) ficaram com o nome original acrescido de .filepart o que inutilizava o reconhecimento dos arquivos por programas que os abriam (ou os reconheciam) diretamente.

Precisei portanto resolver esse problema: renomear várias centenas de arquivos para o nome original SEM o .filepart. Por exemplo:

O arquivo lista_nomes.txt.filepart deveria ser renomeado para somente lista_nomes.txt (que é, ao fim e ao cabo o seu nome original — antes da cópia).

Existem diversas abordagens. Poderia, claro, escrever um script em shell fazendo um laço e, via regex, alterar os nomes individualmente. Quando comecei a codificar vi que levaria um tempo que eu não queria gastar. Então pensei em fazer um script em Python para fazer o mesmo, mas, ainda assim, queria algo ainda mais rápido e, de preferência, SEM escrever um script.

Foi então que lembrei de um comando MARAVILHOSO do Linux em que podemos usar REGEX para alterar nomes: o rename.

O comando rename dá muito mais poder e controle ao usuário na hora de renomear arquivos do que o o mv (normalmente usado para tal — que além de renomear, MOVE arquivos entre diretórios).

Muitas distros já vem com o comando instalado por padrão. Caso a sua não venha (no Mac, que é mais Unix e BSD do que Linux, não vem instalado. Nem no WSL2, diga-se), você pode instalar rapidamente usando o gerenciador de pacotes padrão da distro.

Como eu estava acessando um Mac, usei o brew (caso não conheça esse maravilhoso gerenciador de pacotes para Mac, clique aqui). Depois de instalado a coisa ficou muito mais simples. Supondo que você está no diretório em que deseja alterar os nomes dos arquivos, faça:

rename 's/.filepart//;' *

Simples. Basta isso. Com isso eu renomeei mais de 300 arquivos que estavam com o sufixo .filepart para o seu nome real SEM o sufixo.

Para mais detalhes sobre o rename, digite man rename no terminal ou clique aqui.

Linux é vida!

Se você usa Windows 10, jamais esqueça de explorar o WSL2. Está redondo e bonito! E, principalmente, FUNCIONAL. (daria para ter feito O MESMO rodando o WSL).

Como calcular o custo de um algoritmo?

De forma rápida, existem duas formas de se calcular o custo de um algoritmo:

• Usando o cálculo de complexidade de tempo[1] (em que o custo é expresso por uma função que varia sobre o tamanho da entrada do algoritmo) e
• Usando o cálculo de complexidade de espaço (em que o custo é expresso por uma função que varia também sobre o espaço em memória, primária ou secundária, usado para finalizar o algoritmo).

A mais comum é calcular a complexidade de tempo ou através de uma função de custo associada ao algoritmo[2] ou à complexidade do pior caso expresso em termos da Notação Assintótica do pior caso[3] (que representa um limite superior[4] para o algoritmo).

Para se chegar à função de custo, normalmente se conta quantas instruções são executadas para o algoritmo para resolver um problema. A função de custa é expressa por um polinômio, em relação ao tamanho da entrada.

Por exemplo, no algoritmo

 for(i=0; i<N; i++){
     print(i);
 }

poderíamos dizer que o tempo gasto é

T(N) =
    N*(tempo gasto por uma comparação entre i e N) +
    N*(tempo gasto para incrementar i) +
    N*(tempo gasto por um print)

Isso daria, no caso, a função de custo T(N) em relação ao tamanho da entrada N.

Já a complexidade usando notação assintótica é, geralmente, mais usada para classes de algoritmos por conta da sua simplicidade e abstração. Siga o raciocínio:

Ao ver uma expressão como n+10 ou n²+1, a maioria das pessoas pensa automaticamente em valores pequenos de n. A análise de algoritmos faz exatamente o contrário: ignora os valores pequenos e concentra-se nos valores enormes de n. Para valores enormes de n, as funções n² , (3/2)n² , 9999n² , n²/1000 , n²+100n , etc. crescem todas com a mesma velocidade e portanto são todas equivalentes.

Esse tipo de matemática, interessado somente em valores enormes de n, é chamado comportamento assintótico[5]. Nessa matemática, as funções são classificadas em ordens[6] (como as ordens religiosas da Idade Média); todas as funções de uma mesma ordem são equivalentes. As cinco funções acima, por exemplo, pertencem à mesma ordem.

Essa ideia reflete que precisamos focar, na verdade, em quão rápido uma função cresce com o tamanho da entrada.(essa é a base da “análise de algoritmos” e o centro de como se calcular o custo de um algoritmo).

Nós chamamos isso de taxa de crescimento do tempo de execução. Para manter as coisas tratáveis, precisamos simplificar a função até evidenciar a parte mais importante e deixar de lado as menos importantes.

Por exemplo, suponha que um algoritmo, sendo executado com uma entrada de tamanho n, leve 6n²+100n+300 instruções de máquina. O termo 6n² torna-se maior do que os outros termos, 100n+300 uma vez que n torna-se grande o suficiente. A partir de 20 neste caso.

Abaixo temos um gráfico que mostra os valores de 6n² e 100n+300 para valores de n variando entre 0 e 100:

Podemos dizer que este algoritmo cresce a uma taxa n², deixando de fora o coeficiente 6 e os termos restantes 100n+300. Não é realmente importante que coeficientes usamos, já que o tempo de execução é an²+bn+c, para alguns números a>0, b, e c, sempre haverá um valor de n para o qual an² é maior que bn+c e essa diferença aumenta juntamente com n. Por exemplo, aqui está um gráfico mostrando os valores de 0,6n² e 1000n+3000 de modo que reduzimos o coeficiente de n² por um fator de 10 e aumentamos as outras duas constantes por um fator de 10:

O valor de n para o qual 0,6n² se torna maior que 1000n+3000 aumentou, mas sempre haverá um ponto de cruzamento, independentemente das constantes. E a partir deste valor de cruzamento, 0,6n² sempre crescerá mais rapidamente (e sempre será maior).

Descartando os termos menos significativos e os coeficientes constantes, podemos nos concentrar na parte importante do tempo de execução de um algoritmo — sua taxa de crescimento — sem sermos atrapalhados por detalhes que complicam sua compreensão. Quando descartamos os coeficientes constantes e os termos menos significativos, usamos notação assintótica. Usa-se, normalmente, três formas: notação Θ[7] , notação O[8] , notação Ω[9] .

Por exemplo, suponha que tenhamos nos esforçado bastante e descoberto que um certo algoritmo gasta tempo

T(N) = 10*N² + 137*N + 15

Nesse caso o termo quadrático 10*N² é mais importante que os outros pois para praticamente qualquer valor de N ele irá dominar o total da soma. A partir de N ≥ 14 o termo quadrático já é responsável pela maioria do tempo de execução e para N > 1000 ele já é responsável por mais de 99%. Para fins de estimativa poderíamos simplificar a fórmula para T(N) = 10*N² sem perder muita coisa.

Vamos começar pelo O-grande, que é uma maneira de dar um limite superior para o tempo gasto por um algoritmo. O(g) descreve a classe de funções que crescem no máximo tão rápido quanto a função g e quando falamos que f ∈ O(g) queremos dizer que g cresce pelo menos tão rápido quanto f. (isso é, claro, um “abuso” matemático. Lembre-se sempre que é uma classe de funções, representando um conjunto de funções)

Formalmente:

Dadas duas funções f e g, dizemos que f ∈ O(g) se existem constantes x0 e c tal que para todo x > x0 vale f(x) < c*g(x)

Nessa definição, a constante c nos dá margem para ignorar fatores constantes (o que nos permite dizer que 10*N é O(N)) e a constante x0 diz que só nos importamos para o comportamento de f e g quando o N for grande e os termos que crescem mais rápido dominem o valor total.

Para um exemplo concreto, considere aquela função de tempo f(n) = 10*N2 + 137*N + 15 de antes.

Podemos dizer que o crescimento dela é quadrático:

Podemos dizer que f ∈ O(N²), já que para c = 11 e N > 137 vale

10*N² + 137*N + 15 < c * N2

Podemos escolher outros valores para c e x0, como por exemplo c = 1000 e N > 1000 (que deixam a conta bem óbvia). O valor exato desses pares não importa, o que importa é poder se convencer de que pelo menos um deles exista.

Na direção oposta do O-grande temos o Ω-grande, que é para limites inferiores. Quando falamos que f é Ω(g), estamos dizendo que f cresce pelo menos tão rápido quanto g. No nosso exemplo recorrente, também podemos dizer que f(n) cresce tão rápido quanto uma função quadrática:

Podemos dizer que f é Ω(N²), já que para c = 1 e N > 0 vale

10*N² + 137*N + 15 > c*N2

Finalmente, o Θ-grande tem a ver com aproximações justas, quando o f e o g crescem no mesmo ritmo (exceto por um possível fator constante). A diferença do Θ-grande para o O-grande e o Ω-grande é que estes admitem aproximações folgadas, (por exemplo, N² ∈ O(N³)) em que uma das funções cresce muito mais rápida que a outra.

Dentre essas três notações, a mais comum de se ver é a do O-grande. Normalmente as análises de complexidade se preocupam apenas com o tempo de execução no pior caso então o limite superior dado pelo O-grande é suficiente.

Para algoritmos recursivos usa-se normalmente uma equação de recorrência[10] para se chegar á função de custo. Então, resolve-se essa equação de recorrência para se chegar à fórmula fechada da recorrência.

Muitas vezes é muito difícil se chegar a uma fórmula fechada, então usa-se outros métodos, como a árvore de recursão e o teorema-mestre[11] para se chegar à análise assintótica (usando a notação O-grande).

Exemplos da taxa de crescimento das principais classes de funções

Notas de rodapé:

[1] Complexidade de tempo – Wikipédia, a enciclopédia livre
[2] Análise de Algoritmos
[3] Big O notation – Wikipedia
[4] Limit superior and limit inferior – Wikipedia
[5] Asymptotic notation
[6] Time complexity – Wikipedia
[7] Notação Big-θ (Grande-Theta) 
[8] Grande-O – Wikipédia, a enciclopédia livre
[9] Notação Big-Ω (Grande-Omega)
[10] http://jeffe.cs.illinois.edu/teaching/algorithms/notes/99-recurrences.pdf
[11] Teorema mestre (análise de algoritmos) – Wikipédia, a enciclopédia livre

Essa foi a minha resposta no Quora à pergunta: “Como calcular o custo de um algoritmo”.

Link: https://pt.quora.com/Como-calcular-o-custo-de-um-algoritmo

Qual a utilidade da orientação a objetos na programação, se podemos simplesmente criar e reutilizar funções?

A maior vantagem da Orientação a Objetos é em prover um nível mais alto de Abstração de Dados e a construção e manutenção facilitada de Tipos Abstratos de Dados (TAD).

Não que isso não seja impossível com a programação estruturada (baseada em funções) – mas fazer e construir TAD’s assim, via programação estruturada é mais complicado e com manutenção mais difícil).

Na Orientação a Objetos o nível de abstração é muito maior e a construção de TAD’s (Tipos Abstratos de Dados) fica mais fácil e natural.

Você pode entender um Tipo Abstrato de Dados como uma expansão das capacidades naturais de uma Linguagem de Programação voltada à resolução de problemas reais. Um exemplo clássico é um tipo de dado racional (uma fração).

Originalmente, boa parte das implementações das linguagens de programação imperativas não oferecem esse tipo de dados de forma primitiva (pense em uma linguagem como C que tem 4 tipos de dados básicos ou primitivos: int, char, float e double). A questão de como representar uma fração racional (um número racional) é um problema.

Usamos, então, TAD’s para solucionar esse problema. Você pode pensar em TAD como uma especificação de um conjunto de dados aliado a algumas operações sobre esses dados. Conceitualmente, um tipo de dados (primitivo) da linguagem (como int ou float do C) também tem essa mesma definição: um range (uma faixa) de valores e um conjunto de operações. No caso do int, por exemplo, essa faixa (range) vai de -2.147.483.648 e 2.147.483.647 (que seriam 4 bytes -> 232232 ) e permite as operações de soma, subtração, multiplicação, divisão, incremento e decremento).

Então. Pense em um TAD como essa expansão que permite você representar coisas (abstrações) do mundo real no computador (uma máquina finita e com limitações de memória, hardware, etc.). Então um tipo de dados racional (uma fração) poderia ser definido e representado (em C) através de um tipo composto (um registro/estrutura) da seguinte maneira:

typedef struct { 
    float num;  //seria o numerador da fração
    float den; // obviamente o denominador
}Fracao;  //o nome do novo tipo de dados

Mas, não esqueça, para abstrair tudo certinho o TAD precisa de operações, portanto, em seguida você fazer funções para criação, adição, subtração, multiplicação, divisão, MDC e quaisquer outras que fossem necessárias para complementar o TAD.

Normalmente se faz isso em C em mais de um arquivo, separando a definição do tipo, da sua interface (as suas funções). Isso funciona. Mas, dar manutenção nisso é bem complicado e quaisquer modificações exigiria alterar código em muitos lugares.

Agora pense nisso em um programa de milhares de linhas com centenas de TAD’s criados assim?

Na Orientação a Objetos tanto a abstração da realidade quanto a criação de TAD’s é simplificada no conceito de classe onde tanto a definição do tipo e as operações (as funções, que na OOP chamamos de métodos) estão todas juntas, como uma peça autônoma de código. Quando você altera qualquer comportamento (ou acrescenta ou retira atributos – propriedades) da classe (do tipo) isso é refletido imediatamente em todos os objetos criados a partir deste modelo (deste tipo).

Em uma linguagem Orientada a Objetos como Java, ou Python, ficaria tudo encapsulado/junto em um código só (em um arquivo só). Da seguinte forma (em Java):

class Fracao {
    int num;
    int den;
public Fracao(){ //construtor
    //a regra da criação da fração viria aqui
    //como não poder criar fração com den == 0
}
public adicao(Fracao y){
    //código da soma
}
public subtração(Fracao y){
    //código da soma
}
public multiplicação(Fracao y){
    //código da soma
}
.... //quaisquer outros métodos ou operações
}

Então a resposta é basicamente essa: para fornecer um nível de abstração maior e de construção de TAD’s mais coeso, mais estruturado e mais funcional.

Além disso há a vantagem de representar o mundo real de forma mais semanticamente correta ou parecida (nível mais alto de abstração) e outras potencialidades como a reutilização de código via herança, interfaces, encapsulamento e polimorfismo.

Há desvantagens também. Não é uma panaceia e não resolve todos os problemas de programação do mundo. Mas, para sistemas grandes, complexos e com alto grau de manutenção ela é muito indicada.

Essa é a resposta que dei no site Quora a essa pergunta.

O link original da resposta é:

https://pt.quora.com/Qual-a-utilidade-da-orienta%C3%A7%C3%A3o-a-objetos-na-programa%C3%A7%C3%A3o-se-podemos-simplesmente-criar-e-reutilizar-fun%C3%A7%C3%B5es

Babão, eu? Que nada…

View on Instagram https://ift.tt/2IpyGJJ

Bate papo bom com @juniavasconcelos e João hoje no programa “audiencia publica” sobre “a proteção de dados nas redes sociais, ataques cibernéticos e outros assuntos interessantes.

View on Instagram https://ift.tt/2J4kWB0

Dando um trato nos pelos da face na @sejavikingsbarbearia dos meus alunos Marcelo e Henrique. Passe por lá e confira!

View on Instagram https://ift.tt/2H0hAyZ

Há muitas formas de explicar o amor… Poucas são mais belas que esse sorriso! ❤️❤️❤️😍😍😍❤️❤️❤️

View on Instagram http://ift.tt/2HUFXO0

Hoje faz dez anos que eu disse o sim mais importante da minha vida! Parabéns para nós! Sim para nós! Se Deus permitir, bem vindo aos próximos dez!

View on Instagram http://ift.tt/2pBjY6S